Convex Optimization

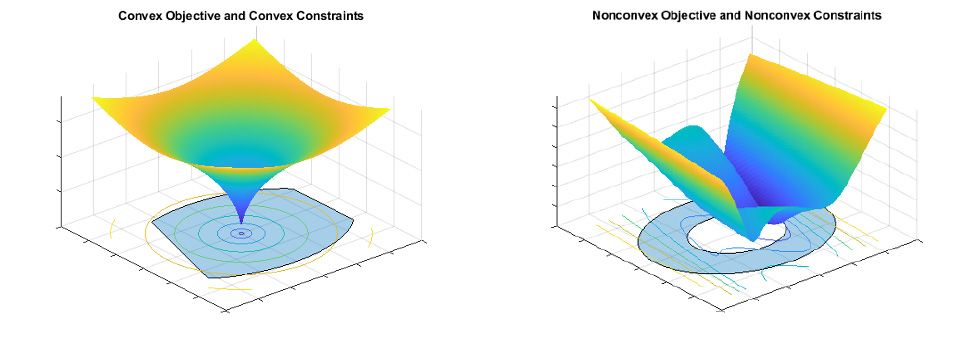
Convex optimization focuses on minimizing convex functions over convex sets, benefiting from the unique geometric and analytical properties of convexity. The field is built on the definitions of convex sets—where any line segment between two points remains within the set—and convex functions—whose epigraphs form convex sets. These structures guarantee well-behaved problem landscapes. A unified standard form allows diverse problems to be reformulated consistently, enabling the application of general-purpose algorithms. This framework’s strength lies in its tractability, as local minima are guaranteed to be global minima, simplifying analysis and computation compared to non-convex problems, which are riddled with local optima and saddle points.

Convex optimization problems are organized into a hierarchy of classes, ranging from linear programming (LP) to quadratic programming (QP), quadratically constrained quadratic programming (QCQP), second-order cone programming (SOCP), and semidefinite programming (SDP). Each class generalizes the previous one, culminating in SDP as the most comprehensive framework. This hierarchy guides solver selection: while a general solver can handle specialized problems, efficiency is maximized when solvers are matched to the simplest applicable class. Alongside this structural classification, optimality is certified by the Karush-Kuhn-Tucker (KKT) conditions. For convex problems, KKT conditions are both necessary and sufficient, offering a mathematically rigorous certificate that a solution is globally optimal. Their connection to duality theory further strengthens the ability to analyze and verify solutions across problem types.

Algorithms bring the theory of convex optimization into practice. First-order methods, like gradient descent, are computationally light per iteration, making them ideal for large-scale applications despite slower convergence. Second-order methods, such as Newton’s method, achieve rapid quadratic convergence but are computationally expensive due to Hessian calculations, suiting smaller, high-precision tasks. Interior-point methods balance generality and efficiency, providing polynomial-time guarantees and broad applicability across problem classes. In practice, these algorithms are accessed through solvers and high-level modeling languages. Modeling tools like CVX and CVXPY, built on the principle of Disciplined Convex Programming (DCP), abstract complexity by automatically verifying convexity and reformulating problems for solvers. A variety of solvers exist, from open-source tools like SeDuMi and SDPT3 to commercial options such as Gurobi and MOSEK, each offering different trade-offs in speed, reliability, and supported features.

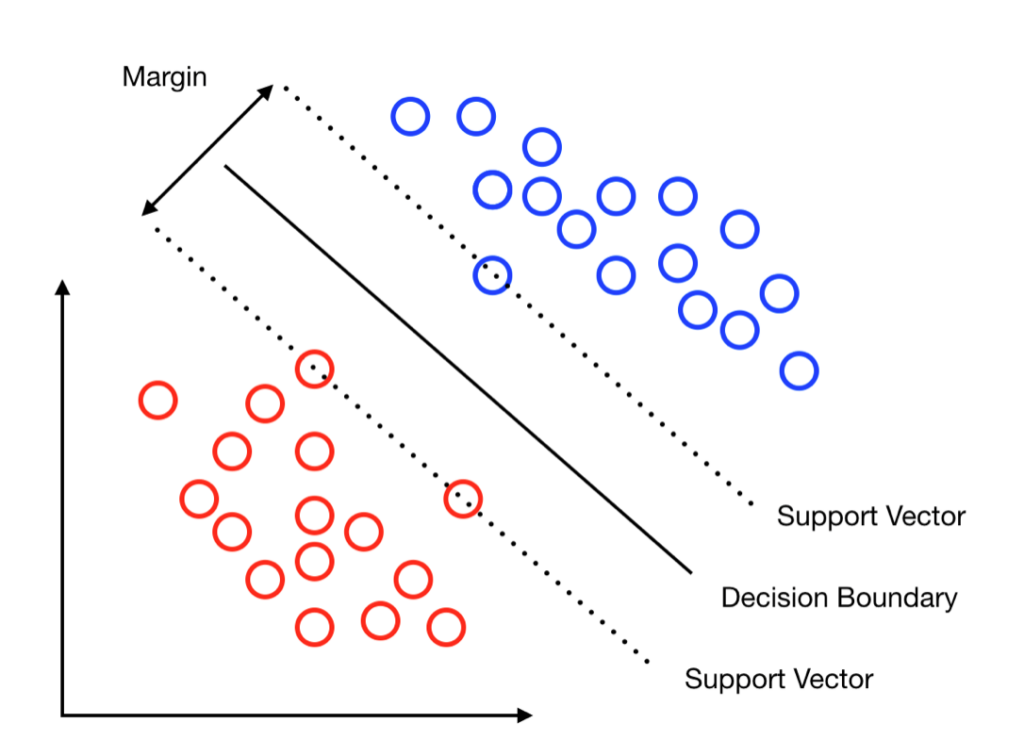
Applications of convex optimization span diverse domains. In communication systems, it powers MIMO channel capacity optimization, also known as the water-filling algorithm. In machine learning, it underpins support vector machines and regression models. Signal processing benefits from convex methods in denoising, deblurring, and waveform design. Beyond natural convexity, the discipline’s versatility is amplified through convex relaxation, which transforms difficult non-convex problems into solvable convex approximations while providing performance bounds. This approach, exemplified by semidefinite relaxations of NP-hard problems, highlights convex optimization’s role as both a direct problem-solving tool and a bridge to tackling otherwise intractable challenges. Its enduring significance lies in combining geometric rigor, algorithmic efficiency, and practical accessibility, establishing it as a cornerstone of modern applied mathematics.